近期帮同学解了一道重邮的Python题目,稍微有点复杂(主要是数学部分),记录于此。
图就不配了,自行脑补(
题目
侯先生每天都会爬楼梯锻炼身体,他有时候一次跨一级,有时候一次跨两级。
有一天侯先生想弄明白一个很难的问题:从最下面的第1级开始到顶端的第n级一共有多少种走法呢?比如n是3时,有两种走法(直接从第1级上跨两步到第3级,或者从第1级跨一步到2级再跨一步到第3级)。
请你帮帮侯先生,给你n (1<n<40)的值,请计算并输出有多少种爬到顶端的方法。
输入n的值,n是1到40之间的整数。
输出一共有多少种从第1级台阶到第n级台阶的走法。
【样例输入】4
【样例输出】3
原题目的用语不规范,没有明确给定侯先生一步最多可以跨多少级。根据题目上下文和示例输入输出可以推测侯先生爬楼梯一步只能跨1或2级。上面的题目已经过修正。
思路1
将台阶看作一个个空位,使用2级尽量填充前面,然后由后至前逐步拆分为1级,拆分出来的1级们又可以组合为2级。遍历并统计所有可能性。
步骤:
- 首先使用2级填充前面的空位,最后如果余下1个空位(奇数级)就填充1级,否则不填充。记录这种排序方法。
- 将最后一个2级拆分为两个1级,这时后面就有了2或3个1级。在保证最左边有1个1级用于与2级间隔的情况下,若后面的1级们又可以组成2级,就尽力组成最多的2级,然后循环遍历。每次得到一种排序就比较记录是否已存在,已存在就continue,否则计数++并记录当前的排序方法。
- 继续拆分,循环遍历……
- ……
这种方法十分复杂,需要用到递归,使问题复杂化,基本不可行。于是抛弃了此思路。
思路2
同样将台阶看作一个个空位,若空位有x个,那么2级最多能有的数量为num_2_max = x // 2。那么2级的数量可以是[0, num_2_max],即0, 1, 2, ..., num_2_max。
遍历2级可能的数量。对于每个2级的可能性数量num_2的情况:
- 由总共的台阶数求得对应的1级的数量
num_1 = x - num_2 * 2。 - 现在有num_1个1级,num_2个2级,加起来刚好可以走完全部台阶。问题可以转化成对这几个1级和2级的排列问题,求得它们的排列的所有可能性就得到了当前
num_2情况下的可能性。 - 累加当前的可能性。
最后即可得到累加的可能性,为总的可能性。
排列数计算
排列数计算方法为:
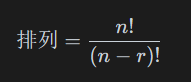
应当注意:所有1级都视为相同的元素(内部顺序不同不会影响结果),因此1级之间不同的顺序不计入结果。2级同理。
由于各种元素内部的顺序不影响结果,我们需要对排列数量进行修正。修正后的排列数量将总的排列数量除以A元素(1级)内部的排列数量和B元素(2级)内部的排列数量来得到。
修正后的排列数为:

完整的排列组合知识点请看排列组合 - OI Wiki (oi-wiki.org)。
代码
import math
def permutation(x, y):
"""计算修正后的排列数"""
total_elements = x + y
inner_permutation_A = math.factorial(x)
inner_permutation_B = math.factorial(y)
corrected_permutations = math.factorial(total_elements) / (inner_permutation_A * inner_permutation_B)
return int(corrected_permutations)
n = int(input())
num_2_max = (n - 1) // 2
probably_counts = 0
for num_2 in list(range(num_2_max + 1)):
num_1 = (n - 1) - num_2 * 2
probably_counts += permutation(num_1, num_2)
print(probably_counts)








Comments NOTHING